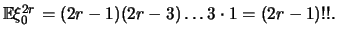A normális eloszlás
A normális eloszláson alapul a statisztika klasszikus elméletének túlnyomó része.
A 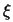 valószínűségi változót
normális eloszlásúnak nevezzük, ha
sűrűségfüggvénye:
valószínűségi változót
normális eloszlásúnak nevezzük, ha
sűrűségfüggvénye:
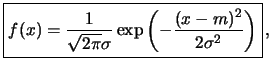
Az 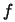 grafikonja az ún. haranggörbe (Gauss-görbe).
Az
grafikonja az ún. haranggörbe (Gauss-görbe).
Az 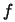 függvény
függvény 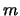 -re szimmetrikus,
-re szimmetrikus, 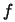 szigorúan monoton növekvő a
szigorúan monoton növekvő a 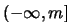 intervallumon.
intervallumon. 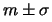 -ban
-ban 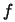 -nek inflexiós pontja van.
-nek inflexiós pontja van. 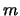 -ben
-ben 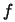 -nek maximumhelye van, a maximum értéke
-nek maximumhelye van, a maximum értéke
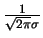 .
. 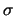 növelésével a harang alakú görbe ,,laposabbá''
válik,
növelésével a harang alakú görbe ,,laposabbá''
válik, 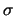 csökkentésével pedig ,,csúcsosabbá''. Az alábbi ábrán
normális sűrűségfüggvények láthatóak
csökkentésével pedig ,,csúcsosabbá''. Az alábbi ábrán
normális sűrűségfüggvények láthatóak 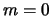 esetén. A legcsúcsosabbnál
esetén. A legcsúcsosabbnál 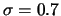 , a középsőnél
, a középsőnél 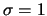 , míg a leglaposabbnál
, míg a leglaposabbnál 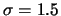 .
.
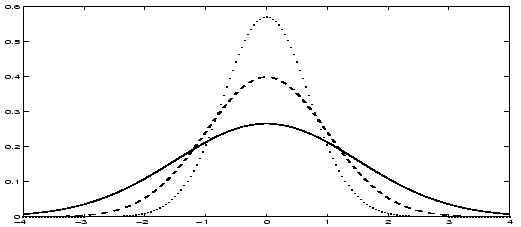
Normális sűrűségfüggvények különböző szórásokra
A normális eloszlásfüggvényre nincs zárt formula, de vannak jó numerikus közelítések.
A normális eloszlás a mérési hibák tipikus eloszlása. Ez a gyakorlatban azt jelenti, hogy ha a mérési eredmények oszlopdiagramját (pontosabban szólva, sűrűséghisztogramját) felrajzoljuk, akkor arra általában jól illeszthető haranggörbe (lásd az alábbi ábrát).
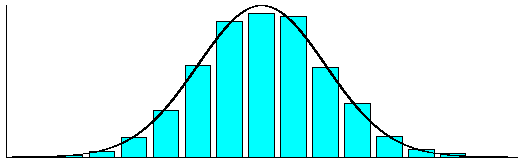
Hisztogram és normális sűrűségfüggvény
A standard normális eloszlás
Ha 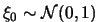 , akkor
, akkor
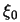 -at standard normális
eloszlásúnak nevezzük. Az alábbi ábrákon a standard normális
eloszlás sűrűségfüggvénye, ill. eloszlásfüggvénye
látható.
-at standard normális
eloszlásúnak nevezzük. Az alábbi ábrákon a standard normális
eloszlás sűrűségfüggvénye, ill. eloszlásfüggvénye
látható.
Az ábrákon bejelöltük a
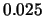 kvantilist:
kvantilist:
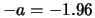 és a
és a
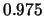 kvantilist:
kvantilist:
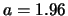 . Ez azt jelenti, hogy a
sűrűségfüggvény alatt besatírozott két rész mindegyike
. Ez azt jelenti, hogy a
sűrűségfüggvény alatt besatírozott két rész mindegyike
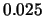 területű. Továbbá,
hogy az eloszlásfüggvény értéke a
területű. Továbbá,
hogy az eloszlásfüggvény értéke a 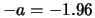 helyen
helyen
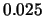 , az
, az
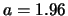 helyen pedig
helyen pedig
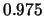 .
.
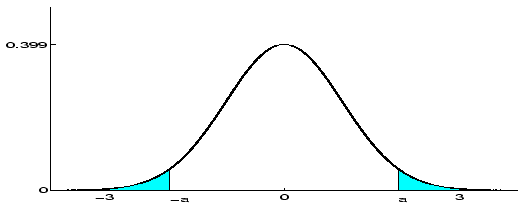
A standard normális sűrűségfüggvény
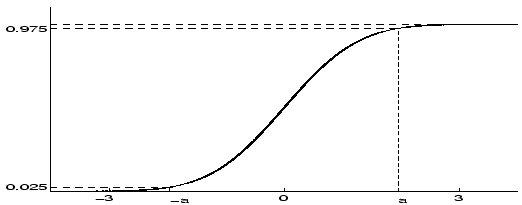
A standard normális eloszlásfüggvény
A standard normális karakterisztikus függvény:
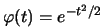 . A páratlan rendű momentumok nullával egyenlőek, a
párosak:
. A páratlan rendű momentumok nullával egyenlőek, a
párosak: