Gyarmati Béla
Minőségügy, kalibrálás és mérési bizonytalanság (3., befejező rész)
Az előző részekben 1 tett fontosabb megállapításaink az alábbiak voltak:
Amiről nem beszéltünk
A bemeneti részbizonytalanságok négyzetes-négyzetgyökös összegzése szigorúan véve csak akkor ad helyes eredményt, ha az egyes összetevők nem korreláltak. Korreláció esetében a bizonytalansági összetevőket ki kell egészíteni - az eredőt sokszor megnövelő - további bizonytalansági összetevővel. Az EA nem tekinti a korrelált változók esetét a főcsapás irányába esőnek, ezért a korrelált változók esetéről csak a D-mellékletben ejt szót.
Érdemes megjegyezni, hogy a két összetevő közti korreláció hiányát (vagy elhanyagolhatóan kicsiny voltát) akkor tételezhetjük fel jogosan, ha az alábbiak valamelyike fennáll:
Az eredő bizonytalanság meghatározása, 2.
Az előzőkben érintettük a bemeneti standard bizonytalanságnak más bizonytalanságijellemzőből (például hibakorlátból) való meghatározását. A bemeneti - mért, vagy csak befolyásoló - mennyiségek standard bizonytalanságainak ismeretében, helyesen felírt mérési egyenlet alapján (a mérési egyenletből rendszerint egyszerűen származtatható érzékenységi együtthatók segítségével) nem nehéz meghatározni az eredő standard bizonytalanságot (és az esetek jelentős részében a korrelációval sem kell foglalkoznunk).
Az eredő bizonytalanságot azonban az EA szerinti szabványos módon nem csak standard bizonytalanság (u) formájában kell közölnünk, hanem úgynevezett kiterjesz tett mérési bizonytalanság (U) formájában is2. (Ez részben egyfajta túlbiztosítás, részben gesztus azok számára, akik másfajta bizonytalansági jellemzőt szoktak meg (például a megbízhatósági [konfidencia-] szintet ...) A kiterjesztett mérési bizonytalanság a(z eredő) standard bizonytalanságnak egy adott (és a kiterjesztett mérési bizonytalansággal együtt mindig megadandó!) k kiterjesztési tényezőnek a szorzata. Az egymással kölcsönösen összefüggő három mennyiség közül bármely kettő ismeretében a harmadik meghatározható3:
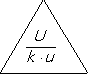
A k kiterjesztési tényező értéke legtöbbször 1,3 és 10 között mozog, de igen sokszor 2-körüli értékű4. A kiterjesztési tényezővel szorzott standard bizonytalanságnak olyan értéktartományt kell meghatároznia, amibe a véletlenszerűen ingadozó eredmények egy megadottnál nem kisebb valószínűséggel mind bele esnek. A szokásos szabványos5 valószínűségi érték 95%.
A kiterjesztési tényezõ meghatározása körüli gondok
Az EA elvárása nem az, hogy mindig (a normális eloszlás 95%-os valószínűségi szintjéhez tartozó) k = 2 kiterjesztési tényezõt használjuk, hanem az, hogy olyan kiterjesztési tényezõt válasszunk, ami az eredõnek az adott esetben indokoltan feltételezhetõ eloszlása mellett közel 95%-os lefedettséget biztosít. Általánosan elterjedt hiba, hogy minden alap nélkül könnyedén tulajdonítanak az eredõ bizonytalanságnak normális (Gauss-) eloszlást, olyankor is, amikor ezt a számítást végzõ hitén kívül semmi sem támasztja alá! 95%-os fedési valószínűség biztosításához a k = 2 tényezõ kizárólag akkor lenne alkalmas, ha az eredõ standard bizonytalanság normális eloszlású lenne, az pedig csak bizonyos jól megfogalmazott (és elég ritkán igazolható) feltételek teljesülése esetében fordul elõ. (Feltételezni ugyan máskor is lehet, de nem lesz hozzáértõ, aki elfogadja …)
Az EA kritériumai az eredõ normalitásának jogos feltételezéséhez:
Minden más esetre a szabadságfokok súlyozott eredõjeként meghatározott egyenértékű (ún. "effektív") szabadságfokhoz tartozó Student-eloszlásnak megfelelõ kiterjesztési tényezõ választandó (amire, sajnos, igaz az, hogy: k > 2), és az EA 6.1 pontjabeli helyett a 6.2-beli szabványmondat alkalmazására van szükség7!
A fenti két módszer (az igazolt normális, illetve a Student-eloszlás alapul vétele) mellett az EA-4/02-ben vannak további ökölszabályok is, amik látszólag jelentõs könnyebbséget biztosítanak. Sajnos, az esetek jelentõs részében az ökölszabályok alkalmazása is olyan feltételekhez van kötve, amiknek a teljesülését igen ritkán lehet igazolni, márpedig anélkül tág tere nyílik az önkényes döntéseknek és hibázásoknak. A különféle egyszerűsítõ feltevésekrõl utólag rendszerint kiderül, hogy valamely részükben nem voltak megalapozottak8.
Sajnos, nem vezetnek helyes eredményre a szokásos numerikus módszerek (konvolúció-számítás, "montekarlózás"stb.) sem! Az eredõ valószínűségi eloszlást ugyan matematikailag látszólag jól lehet közelíteni numerikus módszerekkel, szemléletes görbét kaphatunk az eredõ eloszlás (hibásan számolt!) jellegérõl és meghatározhatjuk a 95%-os lefedettséget biztosító kiterjesztési tényezõt, mégpedig anélkül, hogy az eredõ valószínűségi eloszlását igazából ismernénk. A felrajzolt görbe alakjából ugyan levonható némi következtetés, de a legtöbb eloszlás az elemzõ vélekedésétõl függõen nagyjából egyformán tekinthető (szemre!) egyenletesnek, trapéznak, vagy akár normálisnak is.
Minden módszer, amelyik nem tudja figyelembe venni az egyes összetevõk eltérõ szabadsági fokát, azt eredményezi, hogy az összetevõk szabadságfokainak szóródásától függõen jelentõsen alábecsli az eredõ bizonytalanságot! A numerikus eredõeloszlás-számítás akkor helyén való, amikor vagy minden összetevõ B-típusú, vagy mindegyik A-típusú és egyforma szabadságfokú: sajnos, ez ritka eset!
Az EA "szabványos eljárása"a kiterjesztési tényezõ meghatározására nagyon egyszerű:az egy szabadsági fokra esõ negyedik momentumok összeadhatóságának kimondatlan feltételezésén alapul9:

amibõl az egyenértékű ("effektív") szabadsági fok:
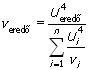
Az egyenértékű szabadságfok birtokában a Student eloszlás szerint a 95%-os valószínűséghez tartozó kiterjesztési tényezõ bármely kézikönyvbõl kiolvasható, de egyszerűség kedvéért itt is közöljük az EA-4/02 E1 táblázatát:
1. táblázat:t95(n) egyes értékei
Egyfelõl, az effektív szabadságfok módszere bármikor alkalmazható, másfelõl nem kell különösebb programozói képesség a feladat programozott megoldásához. A módszer szabványos, könnyű és egyetemes! Mellesleg, az egyenértékű szabadságfokok módszerének az alkalmazásához nincs szükség sem az egyes, sem az esetleges domináns tényezõ eloszlásának jellegén való vitákra:a bemeneti adatok közt nem is kell szerepeltetni az eloszlások jellegét, az eredõ pedig mindig t- (Student) eloszlás lesz10.
Az összehasonlító mérések szerepe
Ha valaki végigkűzdötte magát a kalibrálási eljárás kidolgozásán és
Nyilvánvaló, hogy amirõl nem tudunk, az attól még létezhet:lehet hibás a mérési módszer (például a méréssel szándékolatlanul megváltoztatjuk a mérendõ mennyiség nagyságát), létezhetnek olyan befolyásoló mennyiségek, amikrõl nem tudunk, lehet az etalon hibája nagyobb, mint amit a bizonytalansága alapján neki tulajdonítunk stb.
Ezek a hibák nyilván nem jelennek meg a mérési egyenletben, akkor pedig nem lesznek figyelembe véve a továbbiakban sem, tehát van esélyünk arra, hogy a kalibrált eszköz valódi mérési hibája nagyobb, mint amekkora eltérést az eredõ bizonytalanság alapján valószínűsítenénk!
Az is nyilvánvaló, hogy ha egy bizonytalansági összetevõ nem nulla várható értékű, akkor a nulla várható érték feltételezésére alapított technikák mind torzított eredményt szolgáltatnak. Nemnulla várható értékű bizonytalansági tényezõk esetében a leghelyesebb a várható értékkel való helyesbítés:ha ugyanis tudjuk, hogy mennyi, akkor elvégezhetjük a kiegyenlítését (korrekcióját) . Ha csak felsõ korlátot tudunk rá adni ("nem nagyobb, mint"), akkor a bizonytalanság megfelelõ mértékű megnövelésével kezelhetjük11. A helyesbítés elvégzése alól egyedül az mentesíthet, ha igazolni tudjuk, hogy a torzítás mértéke elhanyagolható (vagy a saját szóródásához képest, vagy az eredõ bizonytalansághoz képest)! Minden más megoldás a mérési bizonytalanságnak vagy az öntudatlan alulbecsléséhez, vagy a piaci esélyeket rontó szándékos túlbecsléshez vezet! (Nem tudom, melyik a rosszabb…)
Mindent összegezve: lehet a bizonytalanságszámítás alapos, "szabványos"stb., de a helyességrõl meggyõzõdni egyedül csak úgy lehet, hogy összehasonlítjuk más kalibrálásokkal12. E más kalibrálások lehetnek ugyanazon labor más eszközzel, vagy más módszerrel stb. végzett kalibrálásai, de metrológiailag sokkal értékesebb a más laboratórium kalibrálásaival való összevetés. Ilyen összehasonlító mérések folyamatosan zajlanak az etalonfenntartók regionális szervezeteiben is. Hazánk az OMH révén az Eurometben számtalan szakterületen tevékeny résztvevõ. A laboratóriumközi összehasonlítással történõ ellenõrzés fontosságát felismerve várja el az EA ezen laboratóriumközi összehasonlító mérések elvégzését (szervezését, illetve a bennük való részvételt). A hazai kalibráló laboratóriumok még nem ismerték fel ezen összehasonlítások fontosságát (aki netán ráébredt, az a NAT-tól várja a szervezést, pedig a kalibrálás alapvetõen öntevékenységet tételez fel).
Elemzett példák
1. példa:kerékpársebesség-mérõ bizonytalansága13
Talán látszólag komolytalannak tűnik ez a példa, de ha alaposan végiggondoljuk, akkor belátjuk, hogy egyrészt, ez is lehet valakinek megoldandó feladat, másrészt e példán keresztül sok lényeges kérdés körbejárható anélkül, hogy a megszokás kerékvályújába csúsznánk. Vegyük tehát komolyan ezt a senki szakterületét nem sértõ példát!
Elöljáróban:a biciklikormányra szerelt, LCD kijelzõs elektronikus bizsu érzékelõje az elsõ kerék villájára szerelten fordulatonként érzékeli a küllõkre pattintott jeladó (állandó mágnes) elhaladását. Egy körülfordulás idõtartama az f frekvenciájú oszcillátor jeleinek leszámlálásával, a jelek periódusideje n-szereseként adódik. Az egy körülfordulással megtett út és az egy körülforduláshoz szükséges idõtartam hányadosa szolgáltatja az adott körülforduláshoz rendelhetõ átlagsebességet. A kijelzõ minden körülfordulás után újraszámítja a sebességet és frissíti a kijelzõt, amelyen 0,1 km/h felbontással leolvasható az éppen érvényes érték. Modellünkben a bicikli sík úton, kőkemény gumikkal, egyenletes sebességgel, egyenesen halad. (Késõbb e feltevések mindegyike fontos lesz!)
A mérés alapjául szolgáló fizikai egyenlet a feltételezett14 működési elv alapján a következõ lehet:
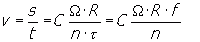
ahol:
s a kerék egy fordulatával megtett út,
t a körülfordulás idõtartama,
C mértékegység-átszámítási tényezõ15,
nagy omega a körülfordulás szöge (névlegesen: 2pi),
R a kerékpár elsõ kerekének aktuális sugara,
tau a belsõ oszcillátor jeleinek periódusideje,
f a belsõ oszcillátor frekvenciája.
Bizonytalanságelemzési célokra a fizikai egyenlet nem alkalmas, mert nem tudjuk vele modellezni sem a belsõ számítás, sem a kijelzés véges felbontását. E bizonytalanságforrásokat azonban már figyelembe vehetjük az alábbi mérési egyenletben:
ahol az elõzõekhez képest a dv tagok a belsõ számításból, illetve a kijelzési felbontásból adódó bizonytalanságot jelenítik16 meg.
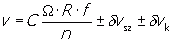
Az egyes összetevõkre vonatkozó érzékenységi tényezõk a fenti mérési egyenlet megfelelõ parciális deriváltjai:
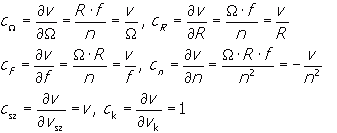
Az egyes bemeneti bizonytalansági összetevõk becsléseit a rendelkezésre álló hibakorlátok, vagy tapasztalati szórások alapján, a következõkben sorra vesszük:
Most már minden együtt van az EA-4/02-szerinti bizonytalansági áttekintõ táblázat (2. táblázat) kitöltéséhez.
Az egyszerűség kedvéért egy további egyszerűsítést teszünk:elhagyjuk a mintatáblázatból az értékek számítására szolgáló oszlopot (mert most nem kalibrálunk, "csak" mérünk, így csak a bizonytalanság meghatározására vágyunk).
Mivel esetünkben egyes érzékenységi tényezõk határozottan sebességfüggõk, ezért nem mindegy, hogy a bizonytalanságszámítást milyen feltételezett sebesség mellett végezzük el!
2. táblázat: Kerékpársebesség-mérõ bizonytalanságszámítása v = 20 km/h sebesség mellett
A 2. sz. táblázatot R = 370 mm kerékátmérõvel (és példaként 20 km/h = 5,56 m/s sebességre vonatkozó adatokkal) töltöttük ki. (A >> jelek az interneten nehezen megjeleníthető "végtelen" szimbóluma helyett szerepelnek.)
Az eredõ standard bizonytalanság a hatodik oszlopban felsorolt járulékok négyzetösszegének négyzetgyökeként (20 km/h sebesség környezetében): 0,023 km/h.
Az eredõ bizonytalanság kiterjesztési tényezõjéhez az egyenértékű szabadsági fok18:
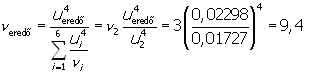
Vigyázat! A 4. hatvány miatt a számítás igen érzékeny, ezért célszerű három-négy értékes jegyű bemenõ adatokkal dolgozni!
A 9,4-hez tartozó Student-tényezõ értéke: t= 2,29. Ez 0,19 km/h eredõ kiterjesztett sebességmérési bizonytalanságot jelent (a kiadódott Student-eloszlás számára a szabványos 95%-os fedési valószínűséggel).
Érdekességként ábrázoltuk a mérési bizonytalanságot is, a sebesség függvényében is19:
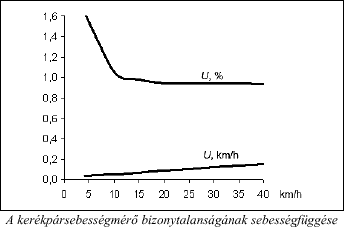
Meg kell jegyezni, hogy az eredmény nem csupán az érzékenységi tényezõk sebességfüggõsége miatt sebességfüggõ, hanem az egyenértékű szabadságfok sebességfüggõsége miatt is (az összetevõk egymásközti arányának változása miatt): 4 km/h-nál veff =145, míg 40 km/h-nál: 7,8.
A görbékbõl jól látható, hogy bár az abszolút (eredõ kiterjesztett) bizonytalanság (alsó görbe, km/h-ban) nem jelentõsen, de függ a sebességtõl. A relatív bizonytalanság (felsõ görbe, %-ban) 10 km/h fölött lényegében 1% (és 10 km/h alatt se nagyon több, mint 1,5%), ami, tekintve a műszer egyszerűségét, olcsóságát, és fõleg alkalmazási célját, azt hiszem, teljesen megnyugtató.
2. példa:Gépjárműsebesség-mérõ kalibrálása
Ez a példa már nem "mérés általában", hanem tényleg szigorúan vett kalibrálás. A rendõrséggel való vitatkozás elõtt érdemes elvégezni autónk sebességmérõjének ("kilométeróránknak") a kalibrálását! Ezt könnyű megtenni, ha rendelkezünk fedélzeti elektronikus motorfordulatszám-mérõvel és elemi gépjárműtechnikai ismeretekkel, no meg némi metrológiai hajlammal... Az elektronikus fordulatszámmérõk ugyanis működési elvükbõl kifolyólag sokkal pontosabbak, mint a műszerfalon lévõ üzemi sebességmérõk, azokhoz képest pontosnak tekinthetõk, reális az esély arra, hogy segítségükkel elvégezhetõ a kalibrálás. Használjuk tehát a gyári fordulatszámmérõt etalonként20!)
A mérés egyenlete:

ahol:
z a hajtómű fõáttételének és a kalibráláskor használt sebességfokozat áttételének az eredõje (z = 4,10)
Az érzékenységi tényezõk rendre:
Az egyes bemeneti bizonytalansági összetevõk becslései:
A fenti adatokkal kitölthetõ a bizonytalansági áttekintõ tábla22:
3. táblázat: Gépjárműsebesség-mérõ kalibrálásának bizonytalanságelemzési táblázata
(A >> jelek az interneten nehezen megjeleníthető "végtelen" szimbóluma helyett szerepelnek.)
A műszerfali motorfordulatszám-mérõnek etalonként való használata révén megállapíthatjuk, hogy a kalibrált sebességmérõ 80 km/h környezetében 0, 38 km/h értékkel pluszszos. (Ez azért lenne jó, mert így a műszerfalról egy adott sebességet leolvasva biztosak lehetnénk abban, hogy azt valójában még nem léptük túl...)
A megállapított sebességeltérés eredõ standard bizonytalansága: u = 0,24 m/s =0,87 km/h.
Az eredõ szabadsági fok23: vegyen =12,4. Az 1. táblázatból a 10-es és a 20-as szabadságfokok közti arányosítással a Student-eloszlás 95%-os valószínűségi szintjéhez adódó kiterjesztési tényezõ k(12,4)95 = 2,24. Az EA szerinti szabványos eredõ kiterjesztett kalibrálási bizonytalanság értéke esetünkben tehát: U = ku =1,8 km/h.
Egy metrológus tudja, hogy hiába van a sebességmérõjében 1,4 km/h tartalék (mivel sebességmérõje a kalibrálás szerint ennyivel többet mutat a valódi sebességnél), ha a(z eredõ kiterjesztett) bizonytalanság ennél nagyobb, akkor könnyen elõfordulhat az, hogy annak ellenére túllépi a sebességkorlátot, hogy látszólag pontosan a megengedett értékkel haladt! Egy metrológus ilyenkor mérlegel...
Csalóka lenne azt hinni, hogy az eredõ közel 2, 5% bizonytalanságot a fordulatszámmérõ 1%-os járuléka érdemben befolyásolná (hogy túl nagy lenne a részesedése)! Ha az eredõt újraszámoljuk pontosnak feltételezett fordulatszámmérõvel, az eredmény akkor is alig változik:az eredõben nem ez, hanem a keréksugár bizonytalansága és a kilométeróra leolvasási bizonytalansága a meghatározó súlyú...
Záró gondolatok
A kalibrálási eredmények hosszas tanulmányozásra érdemesek, mert igen sok hasznos következtetés vonható le belõlük (fentebb ennek bemutatására is tettünk némi szerény kísérletet, de esetenként kiki a saját kérdéseinek megválaszolásához hasznosíthatja az eredményeit). Egy egy kalibrálás befejeztével, a bizonytalanság-elemzések végeztével sose feledkezzünk meg két fontos dologról:
Ezúton fejezem ki köszönetemet azon kollégáimnak és olvasóimnak, akiknek a problémák felismerését és közülük némelyeknek a megértését köszönhetem, és azon olvasóknak, akik e hosszan elnyúlva megjelent tanulmányt végigolvasva figyelmüket a kalibrálással kapcsolatos álláspontom megismerésének szentelték, és akik a várakozás alatt tett észrevételeikkel és javaslataikkal nagyban hozzájárultak ahhoz, hogy ilyen hosszúra nyúljon :-)
- A kalibrálás olyan mérés, melynek tárgya a kalibrálandó eszköz hibája, azaz, bár nem minden mérés kalibrálás, de minden kalibrálás mérés. (Ezért a "kalibrálási"jelző helyett bátran használható a "mérési"jelző.)
- Kifejtettük, hogy a kalibrálási szolgáltatáshoz olyan kalibrálási eljárásra van szükség, ami a labor rendszerezett mérési képességein (mérendõ mennyiségek fajtája, tartománya, mérési bizonytalansága, stb.) alapul, és amit szolgáltatótól "készen" venni igen nagy kockázattal jár. Érintettük a mérési módszer meghatározó szerepét, elemeztük az azt leíró mérési egyenlet jellegét.
- Megkezdtük áttekinteni az eredõ mérési bizonytalanság meghatározásának szabványos eljárását (mindvégig standard bizonytalanságokban gondolkodva).
Amiről nem beszéltünk
A bemeneti részbizonytalanságok négyzetes-négyzetgyökös összegzése szigorúan véve csak akkor ad helyes eredményt, ha az egyes összetevők nem korreláltak. Korreláció esetében a bizonytalansági összetevőket ki kell egészíteni - az eredőt sokszor megnövelő - további bizonytalansági összetevővel. Az EA nem tekinti a korrelált változók esetét a főcsapás irányába esőnek, ezért a korrelált változók esetéről csak a D-mellékletben ejt szót.
Érdemes megjegyezni, hogy a két összetevő közti korreláció hiányát (vagy elhanyagolhatóan kicsiny voltát) akkor tételezhetjük fel jogosan, ha az alábbiak valamelyike fennáll:
- ha az egyik, vagy mindkettő állandó,
- ha értéküket egymás után, egymástól független mérésekkel állapítottuk meg,
- ha az együttváltozás feltételezésére semmiféle okot nem látunk.
Az eredő bizonytalanság meghatározása, 2.
Az előzőkben érintettük a bemeneti standard bizonytalanságnak más bizonytalanságijellemzőből (például hibakorlátból) való meghatározását. A bemeneti - mért, vagy csak befolyásoló - mennyiségek standard bizonytalanságainak ismeretében, helyesen felírt mérési egyenlet alapján (a mérési egyenletből rendszerint egyszerűen származtatható érzékenységi együtthatók segítségével) nem nehéz meghatározni az eredő standard bizonytalanságot (és az esetek jelentős részében a korrelációval sem kell foglalkoznunk).
Az eredő bizonytalanságot azonban az EA szerinti szabványos módon nem csak standard bizonytalanság (u) formájában kell közölnünk, hanem úgynevezett kiterjesz tett mérési bizonytalanság (U) formájában is2. (Ez részben egyfajta túlbiztosítás, részben gesztus azok számára, akik másfajta bizonytalansági jellemzőt szoktak meg (például a megbízhatósági [konfidencia-] szintet ...) A kiterjesztett mérési bizonytalanság a(z eredő) standard bizonytalanságnak egy adott (és a kiterjesztett mérési bizonytalansággal együtt mindig megadandó!) k kiterjesztési tényezőnek a szorzata. Az egymással kölcsönösen összefüggő három mennyiség közül bármely kettő ismeretében a harmadik meghatározható3:
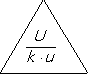
A k kiterjesztési tényező értéke legtöbbször 1,3 és 10 között mozog, de igen sokszor 2-körüli értékű4. A kiterjesztési tényezővel szorzott standard bizonytalanságnak olyan értéktartományt kell meghatároznia, amibe a véletlenszerűen ingadozó eredmények egy megadottnál nem kisebb valószínűséggel mind bele esnek. A szokásos szabványos5 valószínűségi érték 95%.
A kiterjesztési tényezõ meghatározása körüli gondok
Az EA elvárása nem az, hogy mindig (a normális eloszlás 95%-os valószínűségi szintjéhez tartozó) k = 2 kiterjesztési tényezõt használjuk, hanem az, hogy olyan kiterjesztési tényezõt válasszunk, ami az eredõnek az adott esetben indokoltan feltételezhetõ eloszlása mellett közel 95%-os lefedettséget biztosít. Általánosan elterjedt hiba, hogy minden alap nélkül könnyedén tulajdonítanak az eredõ bizonytalanságnak normális (Gauss-) eloszlást, olyankor is, amikor ezt a számítást végzõ hitén kívül semmi sem támasztja alá! 95%-os fedési valószínűség biztosításához a k = 2 tényezõ kizárólag akkor lenne alkalmas, ha az eredõ standard bizonytalanság normális eloszlású lenne, az pedig csak bizonyos jól megfogalmazott (és elég ritkán igazolható) feltételek teljesülése esetében fordul elõ. (Feltételezni ugyan máskor is lehet, de nem lesz hozzáértõ, aki elfogadja …)
Az EA kritériumai az eredõ normalitásának jogos feltételezéséhez:
- mindegyik összetevõnek „jól kezelhetõ” (pl. normális, egyenletes, trapéz vagy háromszög alakú) valószínűségi eloszlásúnak kell lennie,
- mindegyik statisztikailag kezelhetõ („A-típusú”) összetevõ becslése legalább tíz elemű mintából történt
légyen,
Minden más esetre a szabadságfokok súlyozott eredõjeként meghatározott egyenértékű (ún. "effektív") szabadságfokhoz tartozó Student-eloszlásnak megfelelõ kiterjesztési tényezõ választandó (amire, sajnos, igaz az, hogy: k > 2), és az EA 6.1 pontjabeli helyett a 6.2-beli szabványmondat alkalmazására van szükség7!
A fenti két módszer (az igazolt normális, illetve a Student-eloszlás alapul vétele) mellett az EA-4/02-ben vannak további ökölszabályok is, amik látszólag jelentõs könnyebbséget biztosítanak. Sajnos, az esetek jelentõs részében az ökölszabályok alkalmazása is olyan feltételekhez van kötve, amiknek a teljesülését igen ritkán lehet igazolni, márpedig anélkül tág tere nyílik az önkényes döntéseknek és hibázásoknak. A különféle egyszerűsítõ feltevésekrõl utólag rendszerint kiderül, hogy valamely részükben nem voltak megalapozottak8.
Sajnos, nem vezetnek helyes eredményre a szokásos numerikus módszerek (konvolúció-számítás, "montekarlózás"stb.) sem! Az eredõ valószínűségi eloszlást ugyan matematikailag látszólag jól lehet közelíteni numerikus módszerekkel, szemléletes görbét kaphatunk az eredõ eloszlás (hibásan számolt!) jellegérõl és meghatározhatjuk a 95%-os lefedettséget biztosító kiterjesztési tényezõt, mégpedig anélkül, hogy az eredõ valószínűségi eloszlását igazából ismernénk. A felrajzolt görbe alakjából ugyan levonható némi következtetés, de a legtöbb eloszlás az elemzõ vélekedésétõl függõen nagyjából egyformán tekinthető (szemre!) egyenletesnek, trapéznak, vagy akár normálisnak is.
Minden módszer, amelyik nem tudja figyelembe venni az egyes összetevõk eltérõ szabadsági fokát, azt eredményezi, hogy az összetevõk szabadságfokainak szóródásától függõen jelentõsen alábecsli az eredõ bizonytalanságot! A numerikus eredõeloszlás-számítás akkor helyén való, amikor vagy minden összetevõ B-típusú, vagy mindegyik A-típusú és egyforma szabadságfokú: sajnos, ez ritka eset!
Az EA "szabványos eljárása"a kiterjesztési tényezõ meghatározására nagyon egyszerű:az egy szabadsági fokra esõ negyedik momentumok összeadhatóságának kimondatlan feltételezésén alapul9:
amibõl az egyenértékű ("effektív") szabadsági fok:
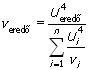
Az egyenértékű szabadságfok birtokában a Student eloszlás szerint a 95%-os valószínűséghez tartozó kiterjesztési tényezõ bármely kézikönyvbõl kiolvasható, de egyszerűség kedvéért itt is közöljük az EA-4/02 E1 táblázatát:
1. táblázat:t95(n) egyes értékei
| v |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
20 |
50 |
>50 |
| t95 |
13,97 |
4,53 |
3,31 |
2,87 |
2,65 |
2,52 |
2,43 |
2,37 |
2,28 |
2,13 |
2,05 |
2,00 |
Egyfelõl, az effektív szabadságfok módszere bármikor alkalmazható, másfelõl nem kell különösebb programozói képesség a feladat programozott megoldásához. A módszer szabványos, könnyű és egyetemes! Mellesleg, az egyenértékű szabadságfokok módszerének az alkalmazásához nincs szükség sem az egyes, sem az esetleges domináns tényezõ eloszlásának jellegén való vitákra:a bemeneti adatok közt nem is kell szerepeltetni az eloszlások jellegét, az eredõ pedig mindig t- (Student) eloszlás lesz10.
Az összehasonlító mérések szerepe
Ha valaki végigkűzdötte magát a kalibrálási eljárás kidolgozásán és
- alkalmas módszert választott,
- valóban figyelembe vett minden szóba jöhetõ bizonytalansági tényezõt,
- helyesen írta fel a mérés egyenletét,
- helyesen határozta meg az egyes érzékenységi tényezõket, sikeresen gyűjtötte össze a bemeneti bizonytalansági tényezõket és rendelte hozzájuk a megfelelõ standard bizonytalanságokat,
- hiba nélkül végezte el az eredõ (standard, majd a kiterjesztett) mérési bizonytalanság meghatározását,
- és ha még a fentieket egy független szervezet (például, de nem feltétlenül a NAT) akkreditálással igazolja is,
Nyilvánvaló, hogy amirõl nem tudunk, az attól még létezhet:lehet hibás a mérési módszer (például a méréssel szándékolatlanul megváltoztatjuk a mérendõ mennyiség nagyságát), létezhetnek olyan befolyásoló mennyiségek, amikrõl nem tudunk, lehet az etalon hibája nagyobb, mint amit a bizonytalansága alapján neki tulajdonítunk stb.
Ezek a hibák nyilván nem jelennek meg a mérési egyenletben, akkor pedig nem lesznek figyelembe véve a továbbiakban sem, tehát van esélyünk arra, hogy a kalibrált eszköz valódi mérési hibája nagyobb, mint amekkora eltérést az eredõ bizonytalanság alapján valószínűsítenénk!
Az is nyilvánvaló, hogy ha egy bizonytalansági összetevõ nem nulla várható értékű, akkor a nulla várható érték feltételezésére alapított technikák mind torzított eredményt szolgáltatnak. Nemnulla várható értékű bizonytalansági tényezõk esetében a leghelyesebb a várható értékkel való helyesbítés:ha ugyanis tudjuk, hogy mennyi, akkor elvégezhetjük a kiegyenlítését (korrekcióját) . Ha csak felsõ korlátot tudunk rá adni ("nem nagyobb, mint"), akkor a bizonytalanság megfelelõ mértékű megnövelésével kezelhetjük11. A helyesbítés elvégzése alól egyedül az mentesíthet, ha igazolni tudjuk, hogy a torzítás mértéke elhanyagolható (vagy a saját szóródásához képest, vagy az eredõ bizonytalansághoz képest)! Minden más megoldás a mérési bizonytalanságnak vagy az öntudatlan alulbecsléséhez, vagy a piaci esélyeket rontó szándékos túlbecsléshez vezet! (Nem tudom, melyik a rosszabb…)
Mindent összegezve: lehet a bizonytalanságszámítás alapos, "szabványos"stb., de a helyességrõl meggyõzõdni egyedül csak úgy lehet, hogy összehasonlítjuk más kalibrálásokkal12. E más kalibrálások lehetnek ugyanazon labor más eszközzel, vagy más módszerrel stb. végzett kalibrálásai, de metrológiailag sokkal értékesebb a más laboratórium kalibrálásaival való összevetés. Ilyen összehasonlító mérések folyamatosan zajlanak az etalonfenntartók regionális szervezeteiben is. Hazánk az OMH révén az Eurometben számtalan szakterületen tevékeny résztvevõ. A laboratóriumközi összehasonlítással történõ ellenõrzés fontosságát felismerve várja el az EA ezen laboratóriumközi összehasonlító mérések elvégzését (szervezését, illetve a bennük való részvételt). A hazai kalibráló laboratóriumok még nem ismerték fel ezen összehasonlítások fontosságát (aki netán ráébredt, az a NAT-tól várja a szervezést, pedig a kalibrálás alapvetõen öntevékenységet tételez fel).
Elemzett példák
1. példa:kerékpársebesség-mérõ bizonytalansága13
Talán látszólag komolytalannak tűnik ez a példa, de ha alaposan végiggondoljuk, akkor belátjuk, hogy egyrészt, ez is lehet valakinek megoldandó feladat, másrészt e példán keresztül sok lényeges kérdés körbejárható anélkül, hogy a megszokás kerékvályújába csúsznánk. Vegyük tehát komolyan ezt a senki szakterületét nem sértõ példát!
Elöljáróban:a biciklikormányra szerelt, LCD kijelzõs elektronikus bizsu érzékelõje az elsõ kerék villájára szerelten fordulatonként érzékeli a küllõkre pattintott jeladó (állandó mágnes) elhaladását. Egy körülfordulás idõtartama az f frekvenciájú oszcillátor jeleinek leszámlálásával, a jelek periódusideje n-szereseként adódik. Az egy körülfordulással megtett út és az egy körülforduláshoz szükséges idõtartam hányadosa szolgáltatja az adott körülforduláshoz rendelhetõ átlagsebességet. A kijelzõ minden körülfordulás után újraszámítja a sebességet és frissíti a kijelzõt, amelyen 0,1 km/h felbontással leolvasható az éppen érvényes érték. Modellünkben a bicikli sík úton, kőkemény gumikkal, egyenletes sebességgel, egyenesen halad. (Késõbb e feltevések mindegyike fontos lesz!)
A mérés alapjául szolgáló fizikai egyenlet a feltételezett14 működési elv alapján a következõ lehet:
ahol:
s a kerék egy fordulatával megtett út,
t a körülfordulás idõtartama,
C mértékegység-átszámítási tényezõ15,
nagy omega a körülfordulás szöge (névlegesen: 2pi),
R a kerékpár elsõ kerekének aktuális sugara,
tau a belsõ oszcillátor jeleinek periódusideje,
f a belsõ oszcillátor frekvenciája.
Bizonytalanságelemzési célokra a fizikai egyenlet nem alkalmas, mert nem tudjuk vele modellezni sem a belsõ számítás, sem a kijelzés véges felbontását. E bizonytalanságforrásokat azonban már figyelembe vehetjük az alábbi mérési egyenletben:
ahol az elõzõekhez képest a dv tagok a belsõ számításból, illetve a kijelzési felbontásból adódó bizonytalanságot jelenítik16 meg.
Az egyes összetevõkre vonatkozó érzékenységi tényezõk a fenti mérési egyenlet megfelelõ parciális deriváltjai:
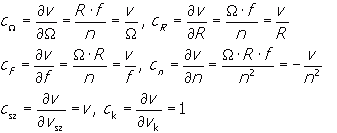
Az egyes bemeneti bizonytalansági összetevõk becsléseit a rendelkezésre álló hibakorlátok, vagy tapasztalati szórások alapján, a következõkben sorra vesszük:
- egy körülfordulás geometriailag szigorúan 2pi radiánnyi, azonban az érzékelõ ezt – feltételezhetõen – nem pontosan érzékeli, tehát értéke bizonytalan: e bizonytalanság felsõ korlátját 20’-re (5,82 mrad) becsülhetjük (ez az érzékelõ által leírt pályaíven több, mint 1 mm, ami valószínűleg biztonsággal nagyobb, mint az érzékelõ billenési bizonytalansága) . Egyenletes eloszlásnál k =gyök(3), így u=5,82/gyök(3) mrad =3,35 mrad,
- a kerék R gördülési sugara – egyenletes terhelés mellett (sík úton!), megdõlés nélkül (egyenesen) haladva – állandó, nagysága a keréktengely közepe és a talaj közti függõleges távolság (a névleges abroncssugárnál a belapulás miatt kicsit kisebb), geometriailag viszonylag könnyen megmérhetõ. Négy mérés szóródásaként a keréksugár standard bizonytalansága: s =1,15 mm,
- az idõmérés pontossági korlátja ma a legolcsóbb kvarcoszcillátorokkal is könnyen lehet jobb, mint havonta ht= ±10 s, amihez uf =9,27 Hz standard bizonytalanság rendelhetõ17,
- az impulzusszámlálás felbontási küszöbe ±1, így a hozzá társított relatív standard bizonytalanságot jogosan tehetjük un =3,32x10-7-re,
- a beépített mikroprocesszor számítási pontosságát 8 digitesre tételezzük fel (a szóban forgó alkalmazáshoz nem kell magasabb szintű számábrázolás). A nyolcdigites számábrázolás relatív hibakorlátja h =2-8, amihez usz =2,26x10-3
- végezetül az LCD kijelzõ utolsó helyi értéke 0,1 km/h, tehát a kerekítési
korlátja 0,05 km/h (0,14 m/s), amihez uk = 0,14/3 0,0802 m/s adódik.
- Az ismétlési bizonytalanság nem volt kimutatható, nulla értékkel való figyelembe vétele csak fölöslegesen bonyolítaná a példát.
Most már minden együtt van az EA-4/02-szerinti bizonytalansági áttekintõ táblázat (2. táblázat) kitöltéséhez.
Az egyszerűség kedvéért egy további egyszerűsítést teszünk:elhagyjuk a mintatáblázatból az értékek számítására szolgáló oszlopot (mert most nem kalibrálunk, "csak" mérünk, így csak a bizonytalanság meghatározására vágyunk).
Mivel esetünkben egyes érzékenységi tényezõk határozottan sebességfüggõk, ezért nem mindegy, hogy a bizonytalanságszámítást milyen feltételezett sebesség mellett végezzük el!
2. táblázat: Kerékpársebesség-mérõ bizonytalanságszámítása v = 20 km/h sebesség mellett
| összetevő |
hibakorlát |
bem.std.bizonyt. |
érz. |
szab.fok |
járulék, mm/s |
| ciklus |
20' |
0,00335 rad |
0,884 m/s |
>> |
2,96 |
| keréksugár |
- |
1,08x10-3 m |
15,02 s-1 |
3 |
17,27 |
| frekvencia |
10 s havonta |
9,27 Hz |
1,34x10-6 m |
>> |
0,01 |
| számlálás |
1 |
0,000802 |
3,19x10-6m/s |
>> |
<0,01 |
| számítás |
8 bit |
1,27x10-6 |
1,000 m/s |
>> |
12,53 |
| kijelzés |
0,1 km/h |
0,00803 m/s |
1,00 |
>> |
0,8019 |
| eredő standard bizonytalanság |
22,98 (0,083 km/h) |
A 2. sz. táblázatot R = 370 mm kerékátmérõvel (és példaként 20 km/h = 5,56 m/s sebességre vonatkozó adatokkal) töltöttük ki. (A >> jelek az interneten nehezen megjeleníthető "végtelen" szimbóluma helyett szerepelnek.)
Az eredõ standard bizonytalanság a hatodik oszlopban felsorolt járulékok négyzetösszegének négyzetgyökeként (20 km/h sebesség környezetében): 0,023 km/h.
Az eredõ bizonytalanság kiterjesztési tényezõjéhez az egyenértékű szabadsági fok18:
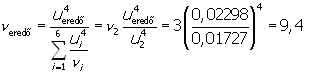
Vigyázat! A 4. hatvány miatt a számítás igen érzékeny, ezért célszerű három-négy értékes jegyű bemenõ adatokkal dolgozni!
A 9,4-hez tartozó Student-tényezõ értéke: t= 2,29. Ez 0,19 km/h eredõ kiterjesztett sebességmérési bizonytalanságot jelent (a kiadódott Student-eloszlás számára a szabványos 95%-os fedési valószínűséggel).
Érdekességként ábrázoltuk a mérési bizonytalanságot is, a sebesség függvényében is19:

Meg kell jegyezni, hogy az eredmény nem csupán az érzékenységi tényezõk sebességfüggõsége miatt sebességfüggõ, hanem az egyenértékű szabadságfok sebességfüggõsége miatt is (az összetevõk egymásközti arányának változása miatt): 4 km/h-nál veff =145, míg 40 km/h-nál: 7,8.
A görbékbõl jól látható, hogy bár az abszolút (eredõ kiterjesztett) bizonytalanság (alsó görbe, km/h-ban) nem jelentõsen, de függ a sebességtõl. A relatív bizonytalanság (felsõ görbe, %-ban) 10 km/h fölött lényegében 1% (és 10 km/h alatt se nagyon több, mint 1,5%), ami, tekintve a műszer egyszerűségét, olcsóságát, és fõleg alkalmazási célját, azt hiszem, teljesen megnyugtató.
2. példa:Gépjárműsebesség-mérõ kalibrálása
Ez a példa már nem "mérés általában", hanem tényleg szigorúan vett kalibrálás. A rendõrséggel való vitatkozás elõtt érdemes elvégezni autónk sebességmérõjének ("kilométeróránknak") a kalibrálását! Ezt könnyű megtenni, ha rendelkezünk fedélzeti elektronikus motorfordulatszám-mérõvel és elemi gépjárműtechnikai ismeretekkel, no meg némi metrológiai hajlammal... Az elektronikus fordulatszámmérõk ugyanis működési elvükbõl kifolyólag sokkal pontosabbak, mint a műszerfalon lévõ üzemi sebességmérõk, azokhoz képest pontosnak tekinthetõk, reális az esély arra, hogy segítségükkel elvégezhetõ a kalibrálás. Használjuk tehát a gyári fordulatszámmérõt etalonként20!)
A mérés egyenlete:

ahol:
z a hajtómű fõáttételének és a kalibráláskor használt sebességfokozat áttételének az eredõje (z = 4,10)
Az érzékenységi tényezõk rendre:
Az egyes bemeneti bizonytalansági összetevõk becslései:
- a sebességmérõrõl való leolvasásnál a skála osztásköze 10 km/h, de gondosan a 80-as "osztásra állva" a szokásos interpolálási bizonytalanság helyett biztonsággal elég lehet 1 km/h hibakorlátot feltételezni, ami egyenletes eloszlás esetén 0,16 m/s standard bizonytalanság.
- a hajtott kerék gördülési sugarának (korrigált tapasztalati) szórása n = 4 mérés eredményeként s = 2,2 mm,
- a fordulatszámmérõ a szervizelésével foglalkozó műhely szerint "a skálaosztásokon jobb, mint 1% pontosságú", ami 3000-es fordulatszám környékén 30 min-1 hibakorlátnak, azaz, egyenletes eloszlást feltételezve 0,144 s-1 standard bizonytalanságnak felel meg21,
- az áttételi viszony a hajtómű fogaskerék-áttételi arányaként teljesen pontosan ismert, így bizonytalansági járulékként 0 értékkel számolhatunk.
A fenti adatokkal kitölthetõ a bizonytalansági áttekintõ tábla22:
3. táblázat: Gépjárműsebesség-mérõ kalibrálásának bizonytalanságelemzési táblázata
| mennyiség |
értéke |
hibakorlát |
bem. std. bizonyt. |
érzékenység |
bizonytalanság, m/s |
szabadsági fok |
| mért sebesség, v= |
80 km/h |
1 km/h |
0,160 m/s |
1 |
0,160 |
>> |
| keréksugár, R = |
29,5 cm |
- |
2,2x10-3 m |
76,6 s-1 |
0,169 |
3 |
| etalon fordulatszám, f = |
3000 min-1 |
1% |
0,144 s-1 |
0,437 m |
0,0629 |
>> |
| hajtáslánci áttétel, z = |
4,1 |
0 |
0 |
1,30 m/s |
0,000 |
>> |
| eredők: e = |
0,38 m/s (1,4 km/h) |
|||||
| u = |
0,241 |
|||||
| v = |
12,4 |
|||||
| U = |
0,540 (1,9 km/h) |
A műszerfali motorfordulatszám-mérõnek etalonként való használata révén megállapíthatjuk, hogy a kalibrált sebességmérõ 80 km/h környezetében 0, 38 km/h értékkel pluszszos. (Ez azért lenne jó, mert így a műszerfalról egy adott sebességet leolvasva biztosak lehetnénk abban, hogy azt valójában még nem léptük túl...)
A megállapított sebességeltérés eredõ standard bizonytalansága: u = 0,24 m/s =0,87 km/h.
Az eredõ szabadsági fok23: vegyen =12,4. Az 1. táblázatból a 10-es és a 20-as szabadságfokok közti arányosítással a Student-eloszlás 95%-os valószínűségi szintjéhez adódó kiterjesztési tényezõ k(12,4)95 = 2,24. Az EA szerinti szabványos eredõ kiterjesztett kalibrálási bizonytalanság értéke esetünkben tehát: U = ku =1,8 km/h.
Egy metrológus tudja, hogy hiába van a sebességmérõjében 1,4 km/h tartalék (mivel sebességmérõje a kalibrálás szerint ennyivel többet mutat a valódi sebességnél), ha a(z eredõ kiterjesztett) bizonytalanság ennél nagyobb, akkor könnyen elõfordulhat az, hogy annak ellenére túllépi a sebességkorlátot, hogy látszólag pontosan a megengedett értékkel haladt! Egy metrológus ilyenkor mérlegel...
Csalóka lenne azt hinni, hogy az eredõ közel 2, 5% bizonytalanságot a fordulatszámmérõ 1%-os járuléka érdemben befolyásolná (hogy túl nagy lenne a részesedése)! Ha az eredõt újraszámoljuk pontosnak feltételezett fordulatszámmérõvel, az eredmény akkor is alig változik:az eredõben nem ez, hanem a keréksugár bizonytalansága és a kilométeróra leolvasási bizonytalansága a meghatározó súlyú...
Záró gondolatok
A kalibrálási eredmények hosszas tanulmányozásra érdemesek, mert igen sok hasznos következtetés vonható le belõlük (fentebb ennek bemutatására is tettünk némi szerény kísérletet, de esetenként kiki a saját kérdéseinek megválaszolásához hasznosíthatja az eredményeit). Egy egy kalibrálás befejeztével, a bizonytalanság-elemzések végeztével sose feledkezzünk meg két fontos dologról:
- A kalibrálás mindig az adott munkapontra vonatkozik, a mérõeszköz minõsítésére még a minõsítési követelmények azonosítása mellett (és az ügyfél igénye ellenére) sem (vagy csak igen korlátozottan) alkalmas,
- A kalibrálással nyert adatok szigorúan véve csak a kalibrálás pillanatában érvényesek, másnap,
vagy a balatoni csúcsforgalomban nem feltétlenül,de az már más megfontolások tárgya kell legyen...
Ezúton fejezem ki köszönetemet azon kollégáimnak és olvasóimnak, akiknek a problémák felismerését és közülük némelyeknek a megértését köszönhetem, és azon olvasóknak, akik e hosszan elnyúlva megjelent tanulmányt végigolvasva figyelmüket a kalibrálással kapcsolatos álláspontom megismerésének szentelték, és akik a várakozás alatt tett észrevételeikkel és javaslataikkal nagyban hozzájárultak ahhoz, hogy ilyen hosszúra nyúljon :-)